 The Gap Theory is one of the unusual teachings Peter Ruckman emphasizes, therefore it merits at least a brief review at Ruckmanism.org.
The Gap Theory is one of the unusual teachings Peter Ruckman emphasizes, therefore it merits at least a brief review at Ruckmanism.org.
What is the Gap Theory? In his excellent book Unformed and Unfilled, Weston Fields provides a brief definition worth noting:
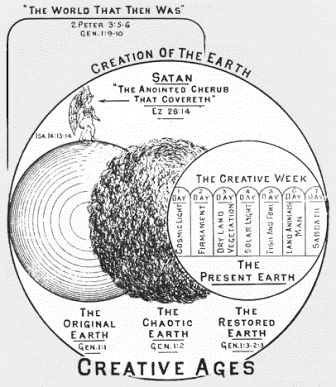
Not all gap theorists agree on the details of the theory, but the one unifying principle of all gap theorists is that Genesis 1:2 (1:1 in the case of the dependent clause view) records the ruin of a once-perfect earth, and a lengthy time-gap between the original creation and the restoration recorded in Genesis 1:3 to the end of the creation narrative. Other details of the theory are mere embellishments and are neither essential to the theory, nor universally held by all gap theorists. (p. 7)
The booklet The Gap Theory by Kent Hovind and Stephen Lawwell describes the origin of the Gap Theory as follows on p. 5:
Thomas Chalmers (1780-1847), a notable Scottish theologian and first moderator of the Free Church of Scotland, is credited with being the first proponent of the gap theory. His proposal of the theory was first recorded in 1814 in one of his lectures at Edinburgh University. Prior to 1814, few theologians considered Genesis 1 as describing anything other than a normal 24-hour, six-day week.
In the Foreword to Weston Fields' book Unformed and Unfilled, John Whitcomb, Jr. has a similar account of the origin of the Gap Theory, and also ascribes the apparent motives:
It was in 1814 that Dr. Thomas Chalmers of Edinburg University first proposed what has since become known as the Gap Theory of Genesis 1:2. By this interpretation of the Bible, Dr. Chalmers felt that he could make room for the vast expanse of time which the geologists of his day were demanding, and at the same time maintain a literal interpretation of the creation account. His views were further elaborated by George H. Pember (Earth's Earliest Ages) in 1876, and enormously popularized by a footnote in the Scofield Reference Bible (first edition, 1917). (p. ix)
Ruckman's views on the Gap Theory are summarized as follows in his own words:
However, Genesis 1:1 refers to a date much earlier, maybe millions of years. Nobody knows the exact time of the original creation of the world in verse 1. Genesis 1:2 is not the original creation, because 2 Peter 3:5-6 tells us something happened to the original creation. Genesis 1:2 says something terrible happened, a great calamity of some kind: "And the earth was without form, and void; and darkness was upon the face of the deep." This is undoubtedly connected with the events of Ezekiel 28 and Isaiah 14, but the event is described even more clearly in 2 Peter 3, and the modern body of apostate fundamentalists who write apologetic literature about the flood have all rejected 2 Peter 3 as referring to Genesis 1:2., which, of course, it does. So, the modern apostate fundamentalist is just as heretical as the modern evolutionist, at least where rejection of the King James text is concerned. This earth was immersed in water in Genesis 1:2, according to 2 Peter 3. (Ruckman, Peter. Theological Studies, Book 16. Pensacola, FL: Bible Baptist Bookstore, 1988, p. 6)
Ruckman's interpretation of 2 Peter chapter 3 here ignores the context of the previous chapter, especially 2 Peter 2:5: "And spared not the old world, but saved Noah the eighth person, a preacher of righteousness, bringing in the flood upon the world of the ungodly;" Ruckman's interpretation seems further unlikely when it is considered that 2 Peter 3:6 (which he lists as telling us what happened with the "original creation") gives the overflowing of water as the cause of the world perishing, which is more naturally interpreted as Noah's flood: "Whereby the world that then was, being overflowed with water, perished:"
If it could be said that Genesis 1:2 raises a question, Exodus 20:11 is typical of a passage in the Bible that answers it: "For in six days the LORD made heaven and earth, the sea, and all that in them is, and rested the seventh day: wherefore the LORD blessed the sabbath day, and hallowed it." Ruckman takes a novel approach in brushing off the truths revealed in Ex. 20:11 by declaring it non-doctrinal! Observe:
Note (!!) that Exodus 20:11 is not a doctrinal statement on the history of creation. If it was, it would be false. There are three heavens after Genesis 1:2. (Bible Believers' Bulletin. August 2002, p. 6)
It is not uncommon for many Ruckmanites to enthusiastically follow Ruckman in his views on the Gap Theory. They quite frequently refer to their view as the "Gap Fact."
Ruckman has used some questionable tactics when attempting to deny what many gap theorists believe. In an article by the title The Mythological “Gap Theory” (Bible Believers' Bulletin. August, 2002) Ruckman makes the following argument:
Page 2: The writer assumes that every Christian who believes in the first chapter of Genesis, AS IT STANDS (see below), thinks that “billions of years passed between Genesis 1:1 and Genesis 1:2.”
They believe nothing of the kind. If you want the time it would be about 2,000 years, making an even 7,000 years between the first creation (2 Pet. 3) and the second creation (Rev. 21)… (p. 1)
First of all, it seems like a straw man argument. Ruckman does not quote much of the context. However, our copy of the booklet he is refuting is unfortunately dated 2006–four years after Ruckman's article–so it could have been revised. Secondly, when Ruckman makes the allegation about how the authors supposedly portray "every Christian," Ruckman does not quote directly. Our copy of the booklet gives a much different impression on that very page:
Those curious will also find that there is a tremendous variation in the accepted duration of the gap. Some proponents of the gap theory feel it only lasted a few hundred years but most believe it lasted millions, if not billions, of years. (Hovind, Kent & Lawwell, Stephen. The Gap Theory. Pensacola, FL: Creation Science Evangelism. 2006, p. 2)
That Ruckman would give only "about 2,000" as the number of years of the supposed gap between Genesis 1:1 and 1:3 in defending the Gap Theory is rather interesting, in light of the other estimates he has given in years past. Notice:
In the Bible account, it could have been here 1,994,000 years (in Gen 1:1) before God recreated it in 6 evening [sic] and mornings, but re-create it He did… (Ruckman, Peter. The Book of Genesis. Pensacola, FL: Bible Baptist Bookstore, 1980, p. 54)
The earth could have been here a good 4,000,000 years before God “recreated it,” in seven evenings and mornings. (Ruckman, Peter. The Book of Genesis. Pensacola, FL: Bible Baptist Bookstore, 1980, p. 4)
However, Genesis 1:1 refers to a date much earlier, maybe millions of years. (Ruckman, Peter. Theological Studies, Book 16. Pensacola, FL: Bible Baptist Bookstore, 1988, p. 6)
It should be no surprise that Ruckman has a sensational view of the mysterious "sons of God" of Genesis 6, and based purely on speculation places them first in the original earth that was supposed to have existed before Genesis 1:3:
Although men were not present before the creation of Adam and Eve, something like men must have been present, for beings called the “sons of God” are mentioned in connection with the Pre-Adamic earth (Job 38:1-8). (Ruckman, Peter. The Book of Genesis. Pensacola, FL: Bible Baptist Bookstore, 1980, p. 5)
A careful student will see that the commission given to Adam is quite similar to the one given to Noah (Gen. 9:1-4). “Replenish” indicates some kind of a previous population… (Ruckman, Peter. The Book of Genesis. Pensacola, FL: Bible Baptist Bookstore, 1980, p. 44)
It is also not a surprise that Ruckman would resort to his crudeness and dogmatism regarding imposing his belief in the Gap Theory on others. Below are a few examples:
Only an apostate Biblical illiterate could fail to see it. [The Gap Theory] We have the “winners,” don’t we, baby?! (Ruckman, Peter. Bible Believers' Bulletin. August, 2002, p. 4)
[Those who disagree with the Gap Theory] …slobbering fanaticism and cultic mentality. (Ruckman, Peter. 22 Years of the Bible Believer’s Bulletin Vol. 1 “The AV Holy Bible” p. 132)
…the modern body of apostate fundamentalists who write apologetic literature about the flood have all rejected 2 Peter 3 as referring to Genesis 1:2., which, of course, it does. So, the modern apostate fundamentalist is just as heretical as the modern evolutionist, at least where rejection of the King James text is concerned. (Ruckman, Peter. Theological Studies, Book 16. Pensacola, FL: Bible Baptist Bookstore, 1988, p. 6)
Considering how vocal Ruckman is in treating those who disagree with him on the Gap Theory, notice what he admits in an apparent unguarded moment about the shaky biblical foundation for the theory (underlining is our emphasis):
The "gap theory" is the teaching that something took place between Genesis 1:1 and Genesis 1:2 that is not explained there but can be inferred from other places in the Scriptures such as Isaiah 14 and Ezekiel 28.
(Ruckman, Peter. The Books of the General Epistles, Vol. 1. Pensacola, FL: BB Bookstore, 2005, p. 461)
The gappers will often try to say that they are interpreting Gen. 1:1-3 in strict chronological order, indicating that there was an original chaotic creation in verse one that preceded the final creation starting in verse three. But a considerable amount of Scripture is not given in strict chronological order. It is generally understood and accepted that the Bible starts off Genesis 1:1 with an introductory statement, not uncommon in other books of the Bible.
Our view is that there is simply too much speculation imposed on the few verses used to support the Gap Theory, to the point that it basically becomes an argument from silence, with a lot of reading between the lines. It is driven not by a desire to interpret the Bible exegetically, but rather in accordance with the conclusions of evolutionary-driven scientists regarding the supposed age of the earth.
This article was not meant to be a comprehensive refutation of the Gap Theory. There is an abundance of good material available on the topic, some of which we recommend below:
Hovind, Kent & Lawwell, Stephen. The Gap Theory. Pensacola, FL: Creation Science Evangelism
Lawwell, Stephen. The Gap Theory: Lucifer's Flood or Church Compromise? Chapel Hill, TN: Echoes of Eden
Fields, Weston. Unformed and Unfilled: A Critique of the Gap Theory. Phillipsburg, NJ: Presbyterian and Reformed Publishing Co.
Thompson, Bert. Popular Compromises of Creation—The Gap Theory http://apologeticspress.org/apcontent.aspx?category=9&article=575
Morris, Henry M. Why the Gap Theory Won't Work. http://www.icr.org/article/why-gap-theory-wont-work/

I do believe that God told Adam to replenish the earth the same word he used for Noah. In Gensis 1:2 And the Spirit of God moved upon the face of the waters' this is the earths condition in 2 Peter 3:5 standing out of thewater and in the water, like a cork, I do believe that this proves that there was a gap. Thank you.
According to Noah Webster's 1828 definition "replenish" simply emans "to fill". The word has changed meaning since then, were it now means to refill. Therefore the use of the word "replenish" in the KJB is not sufficient evidence to prove the gap theory true.
http://webstersdictionary1828.com/Dictionary/Replenish
Good point, thanks.
You may find the following clip interesting.
Thanks. Here is the entire heretical footnote for 1 Corinthians 15:28 in the Ruckman Reference Bible:
(15:28) This is one of those impossible places in the Bible, even when examined and analyzed carefully. The “all things” is obviously a reference to God’s enemies. The Son, of course, is exempted because He is not God’s enemy and He has already subjected Himself to the Father (Phil. 2:7-8). So in the Millennium and the White Throne Judgment God exalts Christ above everything, including the name of Jehovah (Phil. 2:9-11). But in Eternity Christ subjects Himself to the Father once more and goes back into the Trinity as “the Word” (the position He held before He was begotten as the “Son,” John 1:1-3, 14-18). If we are “in Christ,” that would imply that we would go with Him into the Godhead and merge with the Trinity. Now, when I get this far out into infinity and eternity trying to explain a matter as heavy as this one, my standard response is “Ich weiss nicht” (see introduction to Song of Sol.).
Is this the only place where it is found to mean “to fill”? If it is, this is, almost certainly, unreliable at best. The latin prefix re- meaning is again or again and again. I checked many other words in this 1828 dictionary and every one I checked with that re- prefix plus it’s root word had it defined as again. The word replenish was the only one that didn’t. In fact, I couldn’t find refill in this 1828 dictionary. Again, no reliable word even defined that would mean filled again in this 1828 dictionary?
It is way more meaningful to look at the use of replenish in the KJV. Since it used the same term “be fruitful, multiply, and replenish the earth” for Noah after the flood it is much more likely that it means “to fill up again” unless you believe it wasn’t filled up pre-flood.
The Genesis chapter one in my opinion states a fresh begining not a re- begining but now ready to be started not a new but in the begining totally a canvas not ever used previously
Admittedly there are words like replenish used in instructing Adam and Noah
What you do with these should not be put into the first few verses of chapter one.
If we allow ourselves freedom we can make much of if you like about Eve and Satan i.e. Did they have sex together.
So we must not allow ourselves too many unsubstantiated freedoms to make up theories
Otherwise it becomes s woman’s day weekly magazine of gosip : )
I first heard of the "gap theory" from the writings of Finis Jennings Dake. At first glance, I thought, whoah, what is this? But I found his reasonings to make sense especially in the light of the following questions…
Why is Satan (Lucifer) so concerned with this world?
It is obvious that this cherub, (Lucifer) who, before he fell, ruled this world as can be seen from Isaiah 14 and Ezekiel 28…so who exactly did he rule? This period of time was before Adam & Eve since he was already a fallen creature in Adam's Eden, so then who did he rule over? Other angels? Or other beings in addition to angels?
How long was his rule prior to his fall? Hundreds of years? Thousands of years? Millions?
Once he started to rebel in his heart, how long did it take for him to deceive many others into joining him in a futile attempt to overthrow heaven and his subsequent defeat and casting down back to the earth? Who knows how long this would've taken.
Also, once the failed revolt was over, how long was the earth in turmoil prior to full judgement and overthrow of that society that was in existence prior to Adam?
These are all questions that we may need to consider especially since it is obvious that Satan has a strong interest in this world since he was once its physical ruler and even now it's seudo ruler after Adam's forfeit.
So the "gap theory" may not be a theory after all.
Finis Dake was a rank schismatic who promoted a false Christ and was utterly heretical on the Trinity. His perverted notation provided the basis for the Word-Faith error. http://www.pawcreek.org/the-dakes-bible-hagins-and-copelands-doctrines/
Indeed let’s all look carefully at what else did this person or that person think say and do once he/she became a beliver
Let’s just simply life and believe what our Saviour says, do not worry about tomorrow for today has enough concerns of its own.
If we do that, we also defy what the King himself said in Matthew 7.15-20, the following chapter from 6.33-4.
I think it is noteworthy that Ruckman takes the Reformed hermenutic when he defends his heresies, but when he teaches insists on a supremely literal hermenutic described thus:
The infallible rule of interpretation of Scripture is the Scripture itself; and therefore when there is a question about the true and full sense of any Scripture (which is not manifold, but one), it must be searched by other places that speak more clearly. ( 2 Pet. 1:20, 21; Acts 15:15, 16) 1742 Philadelphia Confession I.9.
What a pile of contradictions, as the earstohear YouTube channel might say!
As a firm believer in the Gap Theory (or should I say Gap Fact) over many years, I am saddened that Christians who speak against it – or refuse to study it seriously, fail to take into account ALL the relevant scripture verses that relate to it.
For instance, the passage of KJV scripture below reveals a huge amount of information if analysed carefully:
(2 Pet 3:4-7) "And saying, Where is the promise of his [Christ's Second] coming? for since the fathers [i.e. Abraham, Isaac and Jacob] fell asleep, all things continue as they were from the beginning of the creation [Gen 1:1]. {5} For this they willingly are ignorant of, that by the word of God the heavens were of OLD, and THE EARTH STANDING OUT OF THE WATER and IN THE WATER: {6} Whereby the world that then was, being overflowed with water, PERISHED: {7} But the HEAVENS and the EARTH, WHICH ARE NOW, by the same word are kept in store, reserved unto fire against the day of judgment and perdition of ungodly men."
The points to note from the above are these:
1. At the "beginning of creation" the scripture says, "the heavens were of OLD".
2. In v7 it says, "But the heavens and the earth, which are NOW" – which indicates a different "heavens" and a different "earth" exist NOW – or at the time Peter wrote the scripture.
3. If we read the Book of Revelation, it speaks about a New Heaven and a New Earth:
(Rev 21:1) "And I saw a NEW HEAVEN and a NEW EARTH: for the FIRST HEAVEN and the FIRST EARTH were passed away; and there was no more sea."
The point here is that it appears "the original heaven" was put into a state of judgment a very long time ago and is waiting to be recreated into the form God desires for it to be again as the New Heaven. Somewhat differently, the original earth was put into judgment at the same time as the original heavens as depicted in Gen 1:2; but the earth was restored into its current form as recorded from Genesis 1;3 onwards – which means we are living under "the original heaven" that is still in a state of judgment and on "a restored earth".
After Christ has returned to earth and reigned for 1,000-years, He will restore the original heaven and the restored earth to become the New Heaven and the New Earth "wherein dwelleth righteousness" (2 Peter 3:13). In other words, 'the heaven' that was created originally was put into a state of judgment; and will then be recreated to become the New Heaven. Similarly, the original earth (Gen 1:1) was put into a state of judgment (Gen 1:2); and then recreated as described in Gen 1:3 onwards. The current earth will eventually be burned up with fire (a cleansing or purifying agent – 2 Peter 3:7) and then be recreated into the New Earth.
The 'disaster' mentioned in Gen 1:2 came about after Lucifer was cast out of heaven to the earth (Luke 10:18), and after he had corrupted the then heavens, the earth and its habitants which forced God's judgments to follow. This then produced total darkness in the heavens – which "had no light" and if the earth was viewed from space, it would have had no spherical shape – in other words, "the earth was void" of being recognised as a 'ball' as we would expect to see it today. All that could be seen of the earth from space was light from vocanoes and lava and earthquakes impacting its surface continually as God continued His terrible judgment upon the earth and thereby cleansing it for future restoration commencing at Genesis 1:3. See this for yourself more clearly in the verses below:
(Jer 4:23-26) "I beheld the earth, and, lo, it was WITHOUT FORM [as a sphere], and VOID [of any life]; and THE HEAVENS, and THEY HAD NO LIGHT [meaning, God had turned out light from the Sun, the Moon and the stars. Everything was in pitch darkness!]. {24} I beheld the mountains, and, lo, they trembled [from massive earthquakes], and all the hills moved lightly [from volcanic lava flowing downwards]. {25} I beheld, and, lo, there was NO MAN, and all THE BIRDS of the heavens were fled. {26} I beheld, and, lo, the fruitful place was a wilderness, and all THE CITIES thereof were broken down at the presence of the LORD, and by his fierce anger."
The above description is illustrated on my website here.
In the above verses in Jeremiah 4:23-36, I have found many Christians I share this understanding with prefer to believe Jeremiah's words describe Noah's Flood – while refusing to discuss the issue further. In this, it is clear that the sun rose every day during Noah's Flood, but during this watery flood, there was total darkness – as stated in scripture below:
(Gen 1:2-3) "And the earth was WITHOUT FORM, and VOID; and DARKNESS was upon the face of the deep. And the Spirit of God moved upon the face of the waters. {3} And God said, Let there be light: and there was light."
So for those Christians who refuse to study and discuss this very critical understanding of Creation, the scripture says they are "willingly ignorant" – because they prefer to believe the modern narrative this relates to Noah's Flood rather than what the scriptures plainly say to the contrary:
(2 Pet 3:5-6) "For this they WILLINGLY are IGNORANT of, that by the word of God the heavens were of OLD, and the earth standing out of the water and in the water: {6} Whereby the world that then was, being overflowed with water, perished:"
Thank you for the opportunity to share my understanding of this on your website.
Alan Manson
https://christianspiritwalk.com
2 Peter chapter 3 was already dealt with here, and like Ruckman, you ignored the context starting in the previous chapter. "Whereby the world that then was, being overflowed with water, perished" is more naturally interpreted as Noah's flood, already part of the context (especially 2 Peter 2:5).
Your use of Rev. 21:1 which mentions a new heaven and a new earth in prophecy as proof of the gap theory is mind-boggling. You are simply reading too much into these passages.
Sir, I study the Bible nine times a year. In my archive are some extremely rare writings. Bunyan's Genesis commentary knows NOTHING of a gap, just as Beebe, Knollys, Gadsby, Manton, Dr Gill, Kiffin, Keach, Bakkus, Watson, Ash, Atkinson, Mclean, Tertullian, Montanus, Wycliffe, Coke, Wesley, Trapp, Benson, Poole, Ryle, Edwards, Huss as well as most any other in history because there is no gap, not in English or the original languages. The same thing I say to the continuationist soothsaying heretics I say to you: the verses you are throwing out in the midst of your heresy do not make it so, no matter what appeals to pretexts you make. No Baptist, Puritan, Reformer or fundamentalist has ever taught the gap heresy. You need to repent.
To my critics, I say this.
I mentioned above that in Jeremiah 4:23 it clearly says, "…and THE HEAVENS, and THEY HAD NO LIGHT [meaning, God had turned out light emitted from the Sun, the Moon and the stars. Everything was in pitch darkness!]."
In opposition to this event in the days of Noah's ark floating upon the waters, Noah was able to count the number of days while on board by the periods of daylight and darkness caused by the sun's rotation around the earth, as proven in the verses below.
(Gen 8:6) "And it came to pass at the end of forty DAYS, that Noah opened the window of the ark which he had made:"
(Gen 1:5) "And God called the light Day, and the darkness he called Night. And the evening [darkness] and the morning [light] were the first day."
If the statements made about "…THE HEAVENS, and THEY HAD NO LIGHT" related to Noah's time in the ark as the critics of the Gap Theory claim, it would have been impossible for Noah to count the number of days that he was in the ark; and despite this issue of 'darkness' being discussed on its own, another issue of the ark being in such an environment meant it would have frozen over and become incased in ice due to a lack of heat reaching earth from the Sun. This means that there was another period on earth where there was a massive flood similar to Noah's Flood but was far more devasting.
The scripture verse below illustrates what 'life' was like on the Original Earth prior to this flood occuring:
QUOTE: Jeremiah 4:26 "I beheld, and, lo, the fruitful place was a wilderness, and all THE CITIES thereof were broken down at the presence of the LORD, and by his fierce anger." UNQUOTE
From the arguments presented so far against the Gap Theory, I find its critics ALWAYS avoid making any reference to (or are unwilling to explain their views) on the Jeremiah 4:23-26 verses that prove there was an original flood (known as Lucifer's Flood) that occurred prior to Noah's Flood, which provides a reason why "God created the heavens and the earth" in Gen 1:1, and why it was found to be "without form and void and darkness was upon the face of the deep" in the Gen 1:2.
Maybe someone might like to respond to these comments?
Hi Bro Manson,
Might I suggest that those who hold to the "Gap Theory" VERY rarely take Jeremiah 4:23-26 in its context in the whole chapter of Jeremiah chapter 4??
The whole chapter is about God's judgment of the land of Israel with Gentile invaders from the north, ie. Babylonians. Those verses have NOTHING to do with the events of Genesis chapter 1 brother. I urge you to find me one single verse in Jeremiah chapter 4 that makes any reference to the first chapters of Genesis. It just isn't there brother!
No commentator sees any such thing as well. I've checked John Darby, Cyrus Scofield, Robert Hawker, John Gill, Matthew Henry, John Bunyan whose only commentary is the first ten chapters of Genesis, Dr John Gill, JC Ryle, AW Pink, Johnathan Edwards, Matthew Poole, John Trapp, Thomas Coke, Albert Barnes, Joseph Benson, John Wesley, Hansard Knollys ad infinitum. If there is one, he is not in my archive of over 40 gigabits of the rarest Baptist and Protestant writings extant, a damning witness! I also know of no historian supporting that view; it is a Ruckmanite heresy, yet Ruckman was not the first to proport it. What use is there admonishing an unrepentant man who will not hear?
Hello Nate,
The verses in Jer 4:23-26 speak about:
"…the earth, and, lo, IT WAS WITHOUT FORM, and void; and THE HEAVENS, and THEY HAD NO LIGHT."
On this statement alone, it means that darkness not only existed across the earth, but also across the entire universe and galaxies and not a star to be seen. TOTAL DARKNESS EVERYWHERE!!
In that context, day and night and hence the 24-hour day as we know it no longer existed. When day/night ceases, then time stops (Gen 1:5).
The Bible indicates that such an event has never occurred since the days of Adam and Eve. Even the Jewish calendar acknowledges this claim, as we are in the year 5777.
You can choose to believe this claim or not. If you choose not to, then the following verse may well relate to you:
(2 Pet 3:5-7) "For this they willingly are ignorant of, that by the word of God the heavens were of old, and the earth [as in Jer 4:23-25] standing out of the water and in the water [in Lucifer's Flood whereas Noah's Flood – "the waters covered the earth" – Gen 7:19-20]: {6} Whereby the world that then was, being overflowed with water, perished: {7} But the heavens and the earth, which are now [sine Gen 1:3], by the same word are kept in store, reserved unto fire against the day of judgment and perdition of ungodly men."
Alternatively, I challenge you to show me in scripture WHEN the event occurred where "…the earth, and, lo, IT WAS WITHOUT FORM, and void; and THE HEAVENS, and THEY HAD NO LIGHT" apart from Genesis 1:2.
Blessings!
Hmmm Bro Manson,
Did you ever stop to consider that perhaps these verses from Jeremiah 4 were relating to Revelation 6:12-14??
The burden of proof is on you to give scripture verses PROVING that when the Bible says "the earth WAS without form and void" it really means it "BECAME without form and void". But it doesn't say that, does it? Furthermore, the burden of proof is on you to produce a verse that proves that any gap of time or any events whatsoever occured between verses 1 and 2. There is no such proof, so the Gap Theory is a theory resting on suppositions regarding Genesis 1:2 and Jeremiah 4:23-26, and suppositions alone. There is no PROOF that anything occured between Genesis 1:1 and Genesis 1:2. Even the Lord Jesus places Adam and Eve's creation at the BEGINNING in Mark 10:6. Jesus our Lord knew nothing of any time gap in Genesis. Jesus our Lord does NOT subscribe to the Gap Theory. So, with that, I bid you farewell brother!
Rediculous. Since yesterday, I've been reading quote after quote from the 1800's proving where "King James Onlyism" was very wide spread. See, THE WORD, GOD WILL KEEP IT: by Joey Faust.
That exact book was reviewed here: KJV inerrancy and the ignorance factor in history: Critique of Joey Faust’s book The Word: God Will Keep It https://www.ruckmanism.org/kjv-inerrancy-and-the-ignorance-factor-in-history-critique-of-joey-fausts-book-the-word-god-will-keep-it You are welcome to comment on the book on that specific webpage.
This thread is interesting. I noticed that in regards to 2 Peter 3:5-7 it was said that this section was best taken in light of the context of chapter two and was likely a reference to Noah and the flood. May I simply point point out that this fails in that the context is that of JUDGEMENT (see 3:12 which is yet another judgement) and can be taken as one of different judgements. Especially in light of the fact that 3:1 seems to move into a different idea/thought/JUDGEMENT than that of chapter two. This is not to say the gap theory is correct, but only to say they way the gap theorist interprets chapter three is just as plausible as those who point back to chapter two. To accept or reject the theory cannot be based on this text in isolation because it seems to be a proof text that can be used by either camp and is therefore a neutral text on the subject unless proven otherwise.
At the moment I am on the final leg of a cross-country journey. For a Southerner with Vadious blood, it has been both a blessing and a great interest to see different landscapes for the first time on two Amtrak routes. Trains are amazingly precise; no train waits two hours for one passenger when the train leaves at half past noon. The gap theory like other theological pop theories is most vexatious since it is based on human suppositions rather than inspired, flawless, scripture. When I boarded the train left at the exact time designated on the ticket. There is another exact time barring variables at which it arrives at my destination. The Ruckman railroad through scripture is loaded with pretexted pitfalls to any who dare board his Heresy Express. Frankly, Ruckman's way of arriving at the gap theory is to alter the train's course to a fallacy rather than a destination solidly rooted in Jesus Christ. Could this be why the blessed Master warned so strikingly of both the narrow way and of false prophets whose Broad Way Express is a bullet train into perdition?
Allow me to state when we are asked what Gospel Standard Strict Baptists believe is just so — the very power of God. I am disturbed by any heresy that in any way takes a course apart from, around, over or straight past the gospel. Where did the glorious gospel of peace err? We for 200 years have preached the same message of divine grace without deviation; what is the end of those like ultra-dispensationalists sounding the horn of a false message?
The more one examines sectarian arguments, the more he finds the sectarians are generally incapable of performing great logical feats (Pro. 1.22). If Ruckmanism's poisonous Gap Theory were in scripture, where is the clear verse demonstrating it? Peter had apostolic authority to interpret the Bible on the pain of spiritual anathema if wrong. Why do not the Preterit letters general make mention of a separate flood; though minute, eight chapters is sufficient for a sacred, inspired messenger to make such a distiction? Peter made no such distinction in eight chapters, neither did James, John or Jude, where John has some fifty chapters to make a distinction; the other pair had six chapters, ample space to do so. Saul makes no distinction either in his writings comprising the bulk of the new compact sealed in Jesus' blood shed for many. Conversely, of all the old compact prophets from Abel to Zacharias, there is again no distinction made when the Nohadic flood appears. Manson the unstable soul above isolated several prophets to wrest the scriptures, yet taken in context one finds his views inserted into the text.
This likewise raises a query into Ruckman's genuiness. When he could not support a view, or when he desired to discourage his cultists from examining others who might destroy his view, he labeled them with derision, yet a cursory review of his writings show a morass of contradictions, a likely leftover from his days in Oriental cosmotheistic theosophy. It is interesting how GA Riplinger garnered his praise; her hit piece book "Traitors" cast a large number of men and women out of the undefied church (I smell a popess Joan), for visible or invisible she never specified (see in the Second London Baptist Confession Chapter 26 also Questions 105 and 106 in the 1695 Baptist Catechism as well as Dr Gill's Body of Divinity). This speaks volumes about Ruckman the pseudo-prophet. Thank God Ruckmanism is declining slowly; if only Riplingerism as well as Hylesism would follow suit; yet at the resurrection they shall.
You just contradicted yourself, and therefore cannot be trusted. Besides the Bible tells us Who the accuser of the brethren is. Why would you want to give voice to Him?
Why are you not specific as to a supposed contradiction? Interesting, but very shallow argument that accusing Ruckman is to give voice to the “accuser of the brethren.” I’m sure Ruckman has never accused anyone.
The main problem with the Gap theory is that it is based on a question about a statement in scripture, that is WHY was the earth “without form and void”-Gen 1:2. It is not based on any clear statement of scripture anywhere, such as “the earth became without form and void because of the devil’s rebellion” or anything like that.
It never occurs to the Gap theorist, and it never occurred to Dr. Ruckman, that the earth was without form and void simply because of the fact that God has not yet started to fill it or form it. Indeed, God spends the rest of the chapter telling you how He formed and filled it! The Gap theory simply adds to the word of God!
Your observation makes a lot of sense and does not add or take away from the Scriptures. The gappers will try to say that they are interpreting Gen. 1:1-3 in strict chronological order, indicating that there was an original chaotic creation in verse one that preceded the final creation starting in verse three. But a considerable amount of Scripture is not given in strict chronological order. It is generally understood and accepted that the Bible starts off Genesis 1:1 with an introductory statement, not uncommon in other books of the Bible.
Amen brother!
For years I wondered why there wasn’t an introductory statement declaring that God created the “waters” or the “deep”. So, I was thinking, “Ok, so where did these waters come from?” But it finally occured to me that verse one has already established God as the Creator, so it is another foolish question to ask where the water came from.
It’s really nothing but another bad “shoe-in” for the assumption that says “well, there’s all this water and this deep here, so it must’ve gotten flooded from some previous event”, “darkness represents evil in scripture, so obviously something evil happened”. Again, nothing but conjecture and reading assumptions into the text that aren’t there!
And then, for added disaster, they rip the same phrase “without form and void” from the context of Jeremiah 4, which if read in context, is obvious that Jeremiah is comparing the judgment of Judah and Jerusalem to the unformed and empty state of the first moment of Creation, which they incorrectly describe as “chaotic”; there’s nothing chaotic in Genesis 1:2, it is simply the beginning of God’s creative process!
The Gap theorist completely ignores the context of Jeremiah chapter 4, and makes another assumption. They assume that since the judgment of Judah preceded Jeremiah’s borrowed description from Genesis 1:2, then Genesis 1:2 must also be describing the result of some kind of judgement from God. The vital difference is that Jeremiah 4 is a declarative and clear record of a judgement, whereas there is none mentioned in Genesis 1:1-3 whatsoever. They foolishly take the context and obvious truth of Jeremiah 4 and try to force the same record of judgment into Genesis 1:2.
The Gap Theory is nothing more than a convenient place to dump anything Christians don’t understand about Creation, dinosaurs, astronomy, distant light, and the apprent age of the earth. It’s a bad cop out, and Gap theorists are usually so zealous about condemning others for adding to the word of God- Proverbs 30:-5-6, but then they do the same themselves-Ruckman included. A travesty and the only true gap is their gap in understanding the problem with the Gap Trap!
What I meant above about the argument for the origin of the waters in Genesis 1:2 being “a shoe-in” for the Gap Theory is an argument used to force the conclusion, like someone forcing their way in a room by putting their shoe through the door, not in the traditional sense of “a sure win”.
Just in case there was any confusion in what I meant.
I was recently discussing the Gap theory with a ‘friend’ on Twitter who wouldn’t hear any counterarguments to his pet doctrine, but kept sending me links to articles and videos. I watched and read both. I noticed something important that should be addressed.
Every Gap theorist makes this assumption: the assumption that the phrase “without form and void”- Genesis 1:2, Jeremiah 1:23- means the same as chaos or something that is shambles because of destruction. If you take the words one at a time and study the definition, you see that is not the case at all.
1. “the earth was without form” simply means that the earth was this mass of matter that had no form to it yet. It’s like having a lump of clay that the artist or Potter hasn’t formed into a vase yet. This doesn’t mean that the lump of clay is a lump because someone took some dynamite and blew the smithereens out of a hill of mud lol. The Gap theorist assumes that because God “created” in verse 1 that that means God also must have designed it into a beautiful form as well. It’s another bad assumption, and the Gap theorist ignores the fact that God spends the rest of chapter one explaining how the earth was formed.
2. The word “void” simply means something that is empty, like an empty box. If I look at an empty cave, for example, or an empty lake, I’m not going to automatically assume that some sort of judgement must have taken place to remove every animal or human being from the cave or lake. So, the Gap theorist assumes that if the earth was void, or empty, that must mean that God killed off the inhabitants. Not so! Again, God supplies the next verses explaining that He filled the void earth with trees, beasts, grass, herbs and man!
The Gap theorist asks us to define “without form and void” as chaos or a state of judgment, when that is NOT what the Bible says it is, neither in Genesis OR Jeremiah chapter 4. The Gap theorist asks us to view every verse after Genesis 1:2 as a “Ruin- Reconstruction creation event” when that is NOT what God says it is. Then they like to play games with the differences between the words “create” and “made” and give those words definitions that the word of God nowhere gives.
The Gap theorist is a scripture twisting lunatic and it’s high time God’s people stop pretending that it’s not important or a serious issue just because it’s not a salvation issue! I’m so sick of hearing this cop out. As if adding to the scriptures-Proverbs 30:6- and scripture wresting-2 Peter 3:16 were not serious deeds. I’m not saying that the typical Gap theorist isn’t saved, I believe most of them are. I’m not saying that Pete Ruckman wasn’t saved, I believe he was, albeit off in the head about much! What I am saying is Christians like the Gap theorists have a serious problem with the meaning and authority of Genesis chapter one and have a serious problem with letting their fabricated definitions and theories override the clear wording of scripture.
I’ll stick with the Bible!
“Without form or void” seen in the Masoretic text in the Bible’s second verse is ב וְהָאָרֶץ, הָיְתָה תֹהוּ וָבֹהוּ, וְחֹשֶׁךְ, עַל-פְּנֵי. תּהוּ literally means according to Brown-Driver-Briggs “emptiness” or confusion, so if there was a gap a la Ruckman, CF Parhamn, Michæl Pearl ad nauseum, this couldn’t be since it repeats in different forms twice, תּהוּ & בּהוּ, a double emptiness, a void. Creatio ex nihilo is fact; creation out of creation is fictious myth.
I completely agree with you on that “Old Regular Baptist”.
I’m finally going to say it!!! You know why millions of years were concocted? Why the Gap theory was concocted and invented to soothe confused minds? One word did it! One mystery subject in the life on this planet that is a major stumbling block for many Christians and scientists. With everything I’ve read about the Gap theory and deep geologic time, one topic is always at the forefront of this debate! One group are the poster children for the Gap theory/deep time etc etc: DINOSAURS! THAT’S your problem right THERE! DINOSAURS! Gap theorists can’t explain how to fit these titanic beasts with Adam and Eve because they’ve swallowed every evolutionary lie concerning them! Dinosaurs is your problem! And I’ve seen the proof for what I just said here time and time again…… Let me demonstrate!
If you confess, as a Christian, that you believe in the Resurrection and Divinity of the Lord Jesus here in America, well most Americans will not fight you on it. Tell them you believe in the miracles of the Bible and the prophecies of the Bible and most Americans won’t beat you up verbally too bad, if at all. But the minute you tell most people, even many Christians, that you believe God created dinosaurs with Adam and Eve less than ten thousand years ago and you will be treated like an outcast and an idiot in no time flat! If you don’t believe me, then try it and see. The first thing Gap theorists want to throw in the Gap are the dinosaurs! Every.Single.Time.
Similar to Origen Adamantius’ perpetual creation as well as world prior to the garden enhanced by Ruckman or Parham prior, one must have a gap in his head to think there is a Genesis gap.
If the gap isn't true, what day did God create water?
This is one of those cases where a demand is made upon God which is unnecessary. God already told you that He created the heaven and the earth in Genesis 1:1. God has already established Himself as the Creator. God did not feel the need to express the fact that He also created water and the deep at the same time as well. Genesis 1:2 has to be abused and scripture has to be added to to make the Gap Theory work.
The earth was void and God spends the next several verses telling you how He filled it. The earth was without form, and God spends the next several verses telling you how He formed it. There was darkness because God had not yet called the Light til the next verse. Lucifer doesn't fall until Genesis 3 when he tells Eve that God is a liar. One third of the angels don't fall until Revelation chapter 12, which is a still future event for the same reason that Revelation chapter 9, 10, 11 area still future. The Gap Theory doesn't account for anything and is nothing but an unscriptural fantasy!
Good observations. Thanks for your post.
Maybe there should be tap dancing music playing when you give that answer. If I asked you what day the sun was made, or fish, you could give me the answer, but water is there before day one, and when it is mentioned it is just separated.
Hi Steve,
Yet Exodus 20:11 says that God made the seas, which is the gathering together of waters, during the six days. So for those who believe in the Gap, the burden of proof is to produce a single verse that says the waters existed before the six days. With one verse-Exodus 20:11, God has filled in the Gap. It's nothing but a fantasy for those who have an invented problem with geology and dinosaurs.
If that reponse is not enough, then please consider that Exodus 20:11 also says "and all that in them is". With that single phrase in that single verse, God has destroyed the Gap theory. Genesis 1:1-2 is simply a two verse introduction to what God does in the next 29 verses. He tells you it was without form and void and then spends the next 29 verses telling you HOW He formed and filled it. It's that simple. All the Gap theory does is muddy the waters for people who don't want to pay any attention at all to those 29 verses.
Amen brother, It's even simpler, Revelation 21:1, proves there was and is only one earth, therefore, no gap!
"And I saw a new heaven and a new earth: for the FIRST heaven and the FIRST earth were passed away; and there was no more sea."
Thank you Nate. GAP was introduced to work “millions of years” into the Bible. If we just take the Bible literally we cannot tolerate GAP. Also, in Genesis 2:7, some Gappers like to say there is another creation of man, but that is a literary device known as “prolepsis.” Very commen in Oriental writing. A restatement of something that already happened.
An example would be “When my husband was 4, he had a toy machine gun.” Looking at that statement closely, it is obvious that when he was 4, he was not my husband! That is prolepsis.
Webmaster, you used to have a link where you could suggest an article for the site. I have two suggestions that I think would be really helpful. 1. Write an article explaining how Ruckman's views actually contradict his "King James Only" stance since he added to the King James Bible so many ridiculous ideas and 2. Show the absurdity of Ruckman's claim that Behemoth is Satan. Thanks
Your first suggestion is somewhat covered throughout various articles, although in an indirect way. I might take a stab at what you suggest.
As to Ruckman’s claim that Behemoth is Satan, it is something that did not stand out to me, possibly because it fell through the cracks among so many other bizarre teachings. I suppose he brings that up in his Job commentary. I will read what he says and see if it motivates me to write on it. Thanks for the suggestions.
Gap theorists claim that when God told Adam and Eve to replenish the earth, He was telling them to refill the earth with something that had been here BEFORE Genesis 1:2. Gappers claim that was angels and dinosaurs, so were Adam and Eve expected to replenish the earth with angels and dinosaurs? See, the Gap theorists never take their theory to its absurd conclusions!
The command to replenish the earth simply meant to replant the crops that they and their multiplied children were going to stuff their faces with that God had put in the ground in the first place. Genesis 2:5 makes that abundantly clear. It has absolutely. NOTHING to do with refilling anything that supposedly was here before Genesis 1:2. The Gap theorists, led mainly by Jimmy Swaggert and Ruckmanism, are simply inventing fantasies and problems where there simply are none in the plain Genesis text!
I would be interested in finding out in the comments if the Gap believers are PBI Graduates or not?
Every Bible verse is from the infallible Word of God. The KJV.
Genesis 2:4 says, "These are the generations of the heavens and of the earth when they were created, in the day that the LORD God made the earth and the heavens,"
By the time we get to Genesis chapter 2… The BIBLE said, "these are the GENERATIONS (PLURAL) of the heavens AND (did you see the word AND???) the Earth" ???
There were ALREADY "generations" of the "EARTH" by Genesis chapter 2!
Generations is more than one generation (notice the, "S" at the end of the word).
That is what the Bible says!
Immediately AFTER Adam and Eve were created… God said, "These are the generations of the earth"
Explain THAT anti gappers!!
Please try to explain it without changing the bible this time.
And while we're are it… If God meant to tell Adam and Eve to, "fill" the earth instead of "REPLENISH" the earth, then why did God use the word, "FILL" in Genesis chapter 1, verse 22???
God used the word, "fill", and the word, "replenish" in very same same CHAPTER!
Within 7 verses of each other!!
God said to, "FILL" the waters of the sea in verse 22! Then he says to "REPLENISH" the earth in verse 28!!
If God wanted to use the word, "FILL" instead of the word "REPLENISH", he would have!
You automatically know someone is promoting a false doctrine when they start changing the word of God with Hebrew, or Greek, or a dictionary, or their own opinions.
God said, "replenish". He meant "replenish". He did NOT mean, "fill" in verse 28!
When you have to change what God said to prove your argument… You automatically lose.
God told Noah to, "replenish" the earth because the EARTH was inhabited BEFORE the flood.
God told Adam and Eve to, "replenish" the earth because the EARTH was inhabited BEFORE they were created.
Why do some of you have such a hard time just believing the Bible???
For me the gap theory answers some questions, such as when did Satan fall? As it appears to have happened before the fall of Adam, given Satan already having sin by deceiving Eve. It would also give an explanation to why there are so many dinosaur bones, as it seems creatures existed before Adam. Suffice to say which is the right answer? I don't know but either one, gap or not is compatible with the Bible, and if it helps a believer to have peace over all the scientific misinformation out there (ie the scientific belief that evolution is fact) then I'm not sure the harm it causes.
Gen 1
27 So God created man in his own image, in the image of God created he him; male and female created he them.
28 And God blessed them, and God said unto them, Be fruitful, and multiply, and replenish the earth, and subdue it: and have dominion over the fish of the sea, and over the fowl of the air, and over every living thing that moveth upon the earth.
29 And God said, Behold, I have given you every herb bearing seed, which is upon the face of all the earth, and every tree, in the which is the fruit of a tree yielding seed; to you it shall be for meat.
This arguement becomes quite simple when one reads the bible for what it says , the word is "replenish" and it means just that . Take into account what God says "herb bearing seed"and "tree yielding seed" . The herbs and trees come with seeds, they are for food , and from which come seeds for planting . God now provides an example by planting a garden Himself . Notice the bible says He planted a garden , not spoke it into existence . The river that waters the garden in Eden now goes outward to water man's garden.
Gen 2
8 And the LORD God planted a garden eastward in Eden; and there he put the man whom he had formed.
9 And out of the ground made the LORD God to grow every tree that is pleasant to the sight, and good for food; the tree of life also in the midst of the garden, and the tree of knowledge of good and evil.
10 And a river went out of Eden to water the garden; and from thence it was parted, and from thence it was parted , became into four heads.
And there we have a simple staight forward explanation of "replenish" with the example coming from God Himself. [Message edited only to remove junk HTML code]
The Hebrew word underlying replenish in Gen. 1:28 is maw-lay, which was often translated as filled in the KJV, which is the primary meaning of said Hebrew word. Theological disputes should be settled by the Word of God in the original languages when possible, not by translation choices of an English translation when other forms of translation for a given passage under dispute are also valid. Many Ruckmanites speak disparagingly of “going to the Greek,” as if that is a no-no, but I could demonstrate case after case in which Ruckman did exactly that when it was convenient.
Replenish means “to make replete.” If you read Chaucer you will get this.
If you eat a big meal you are “made replete,” or entirely filled. You are replenished. You are still you, you did not need to be killed to be replenished.